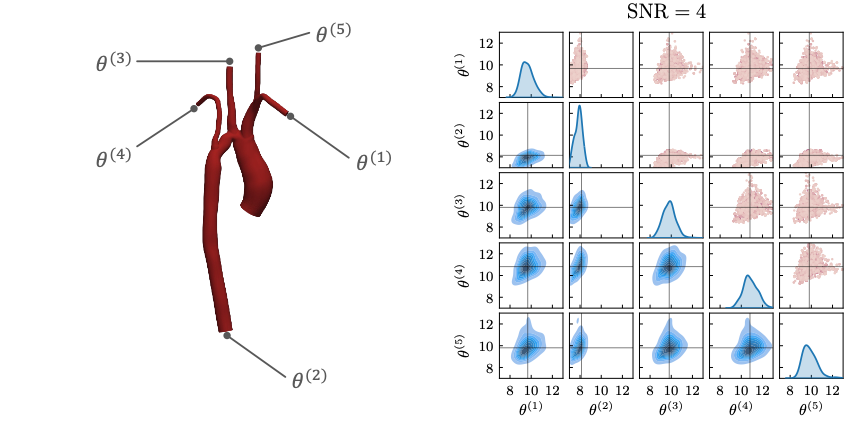
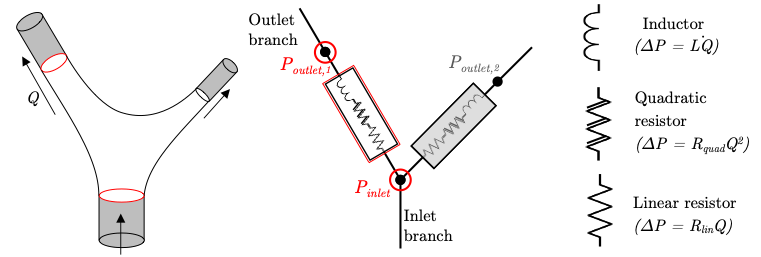
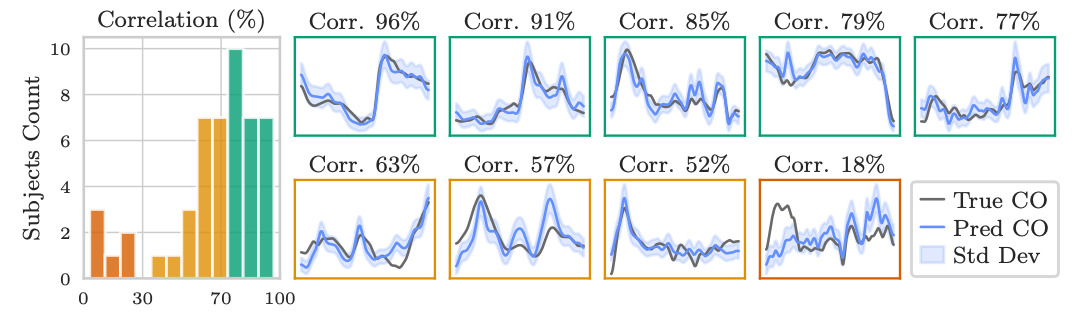
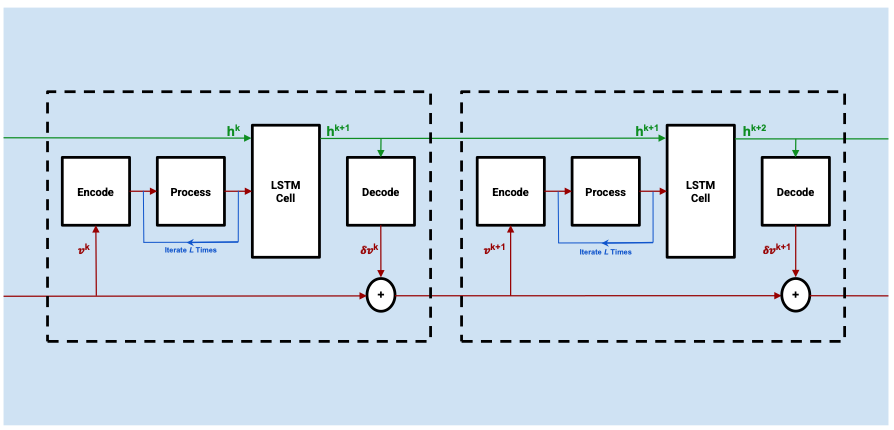
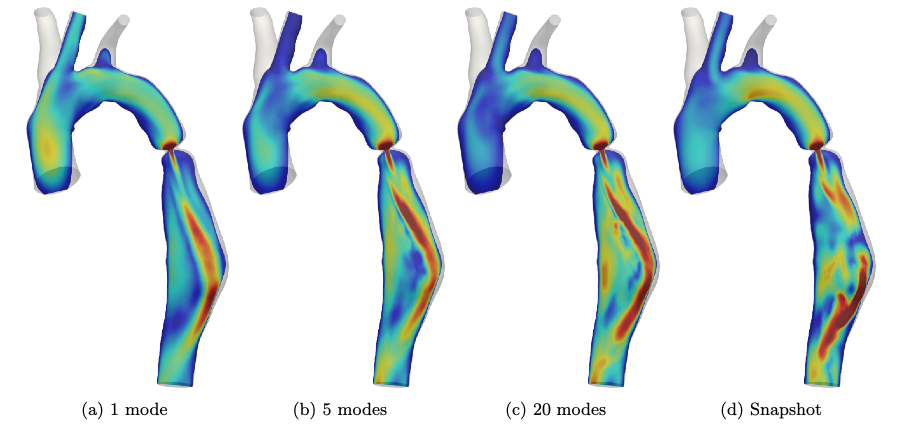
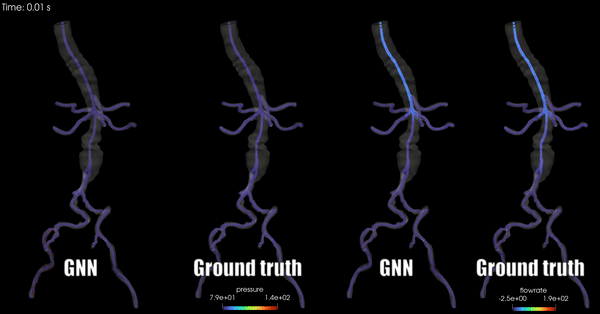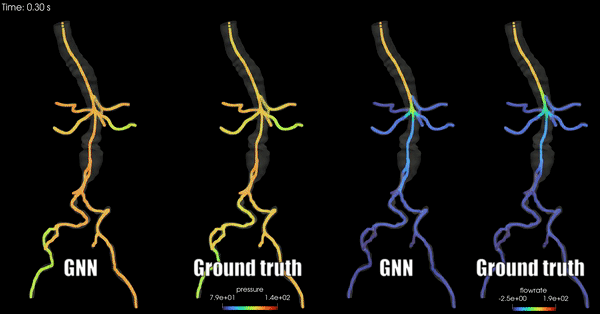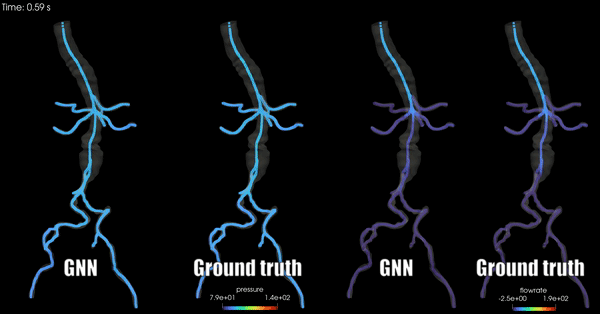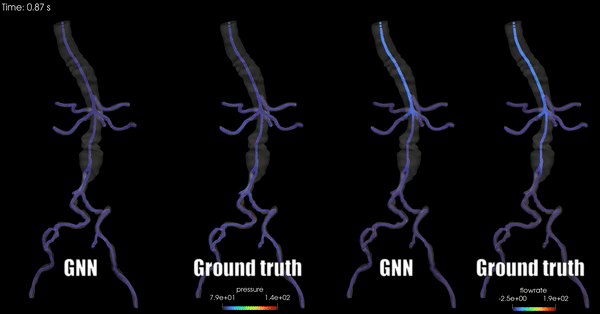
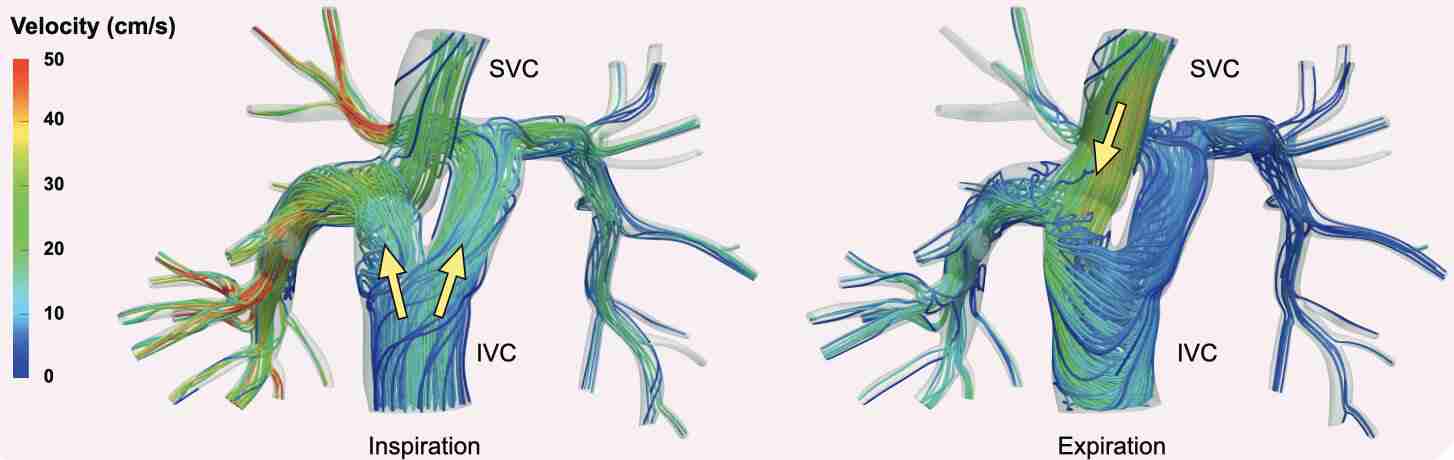
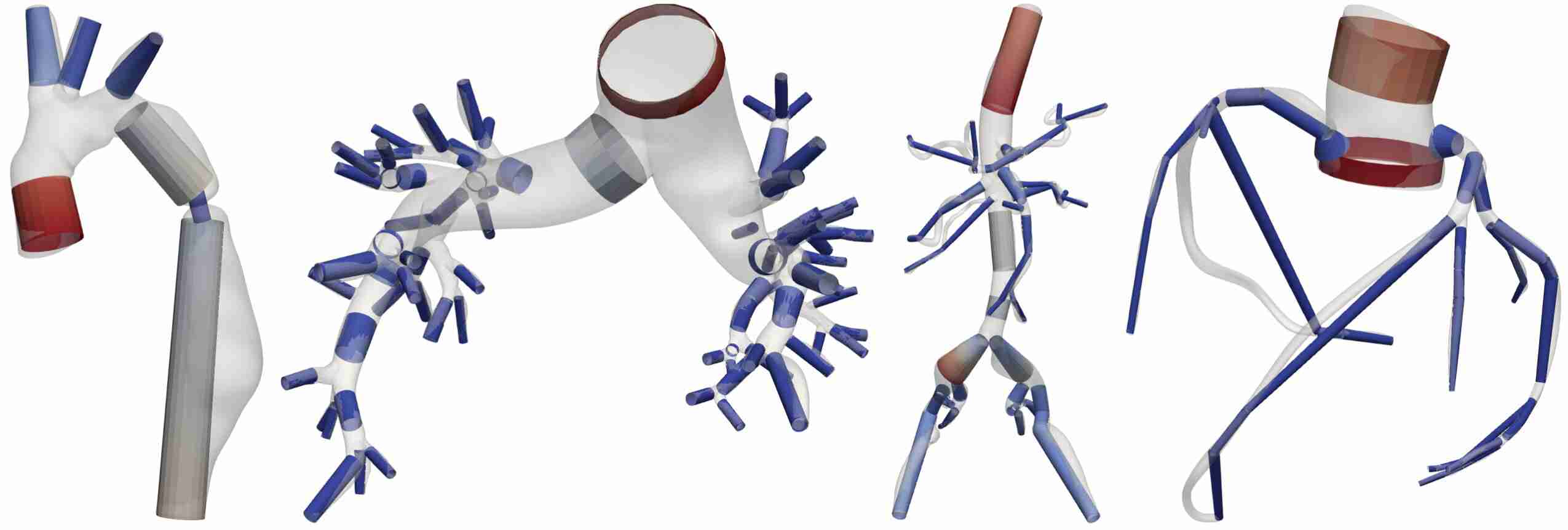
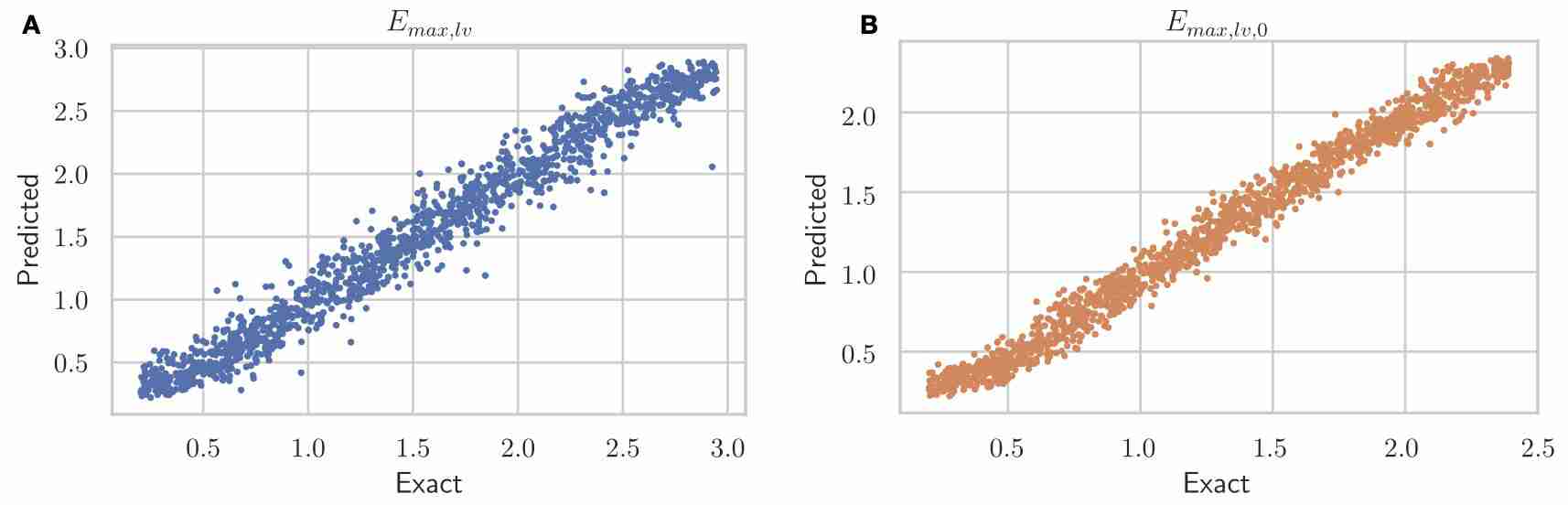
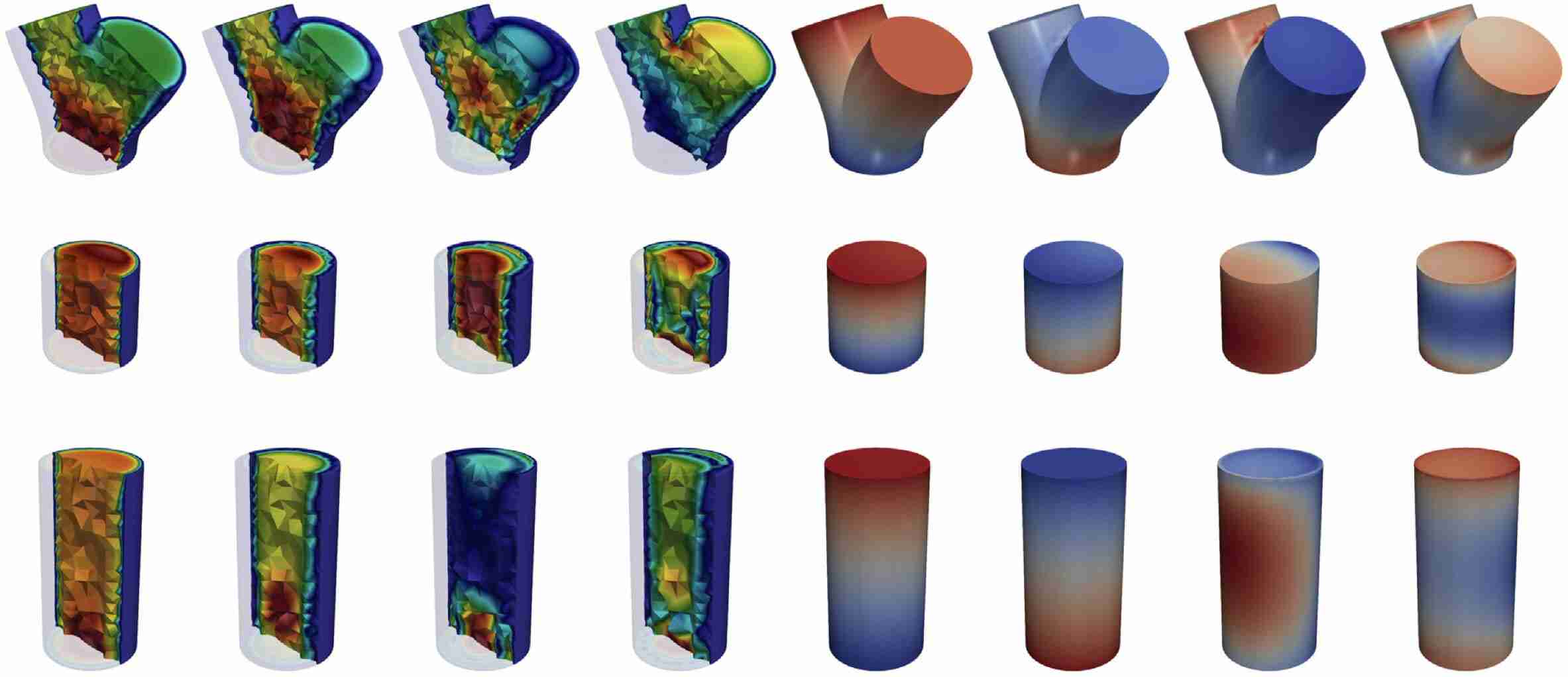
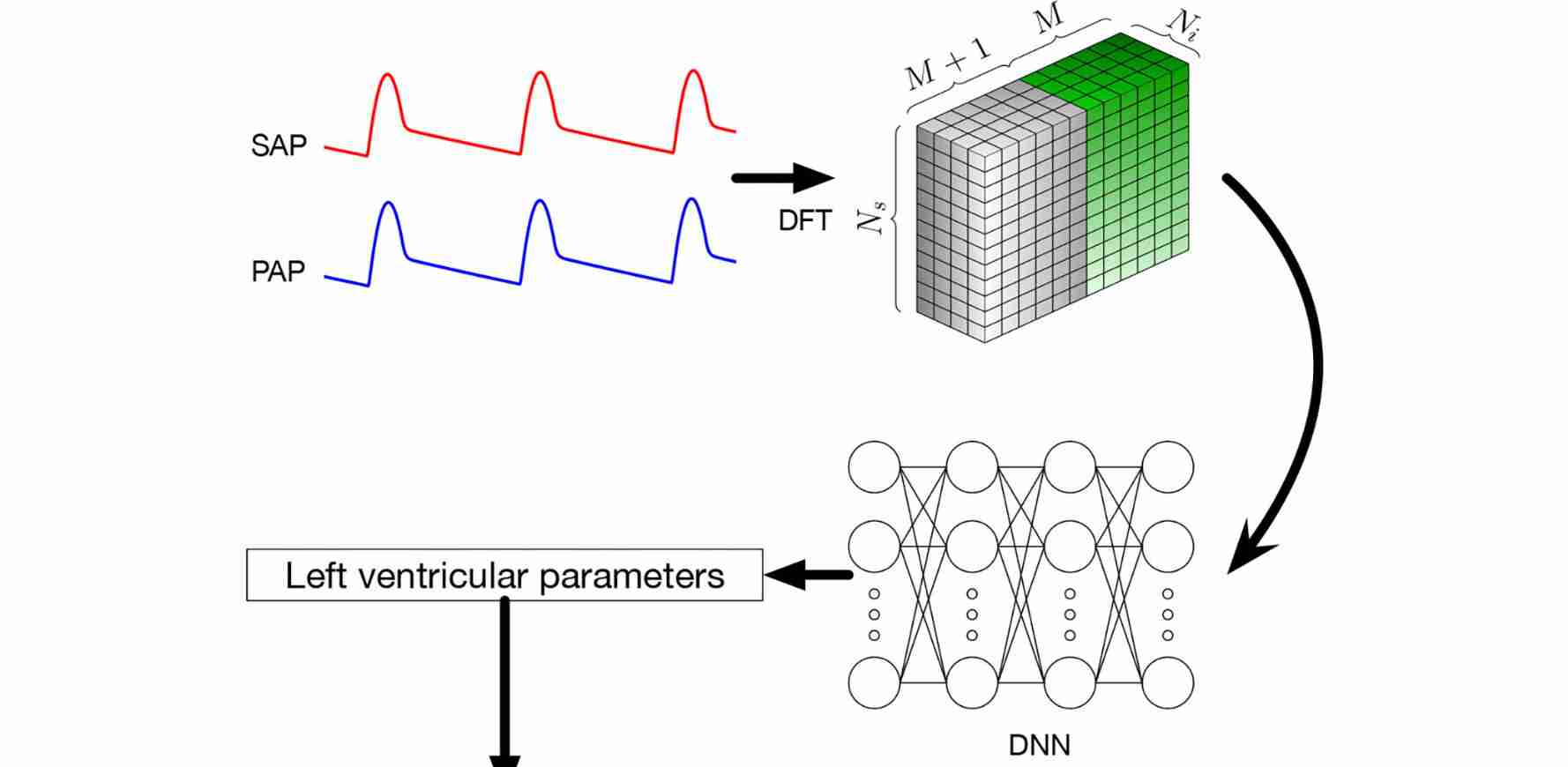
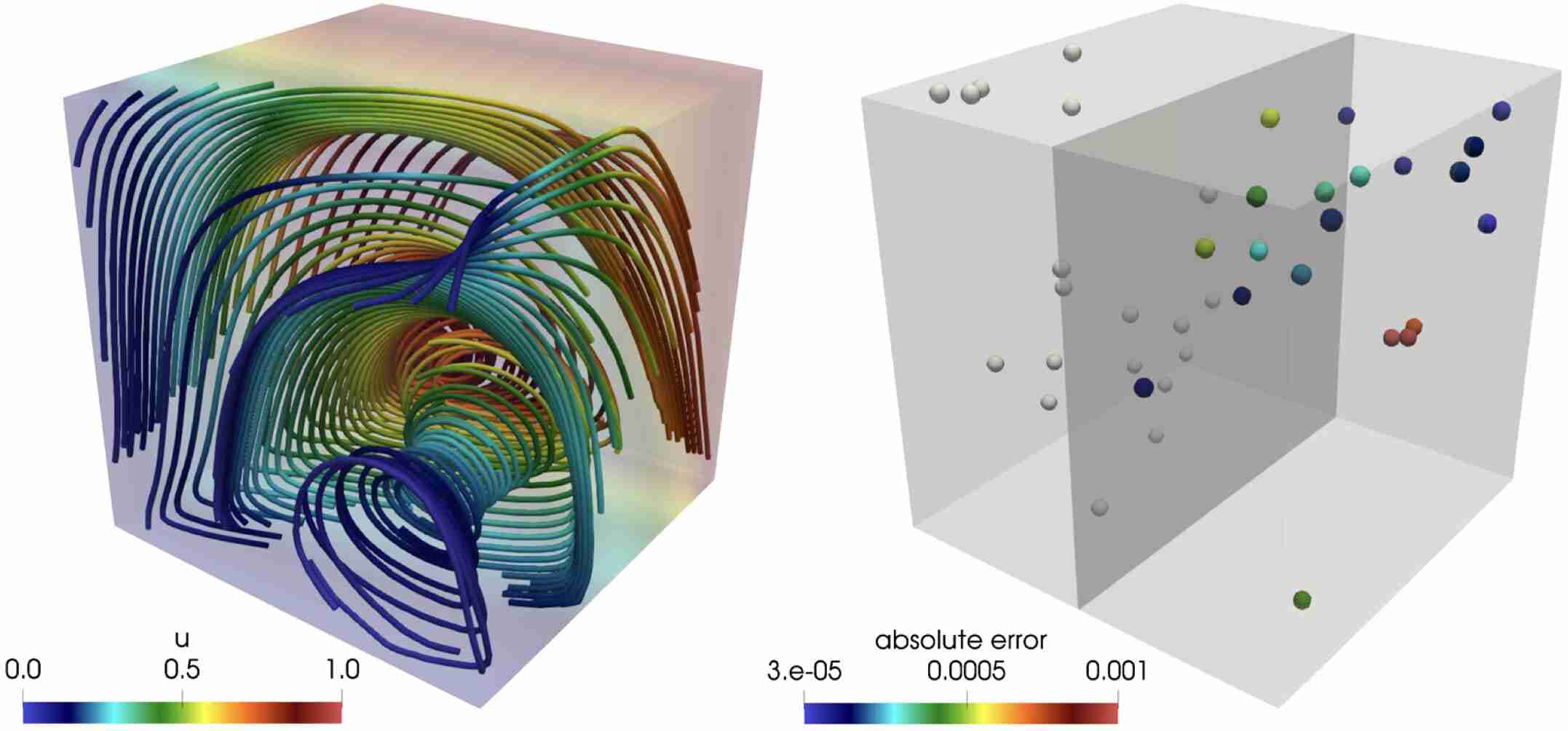
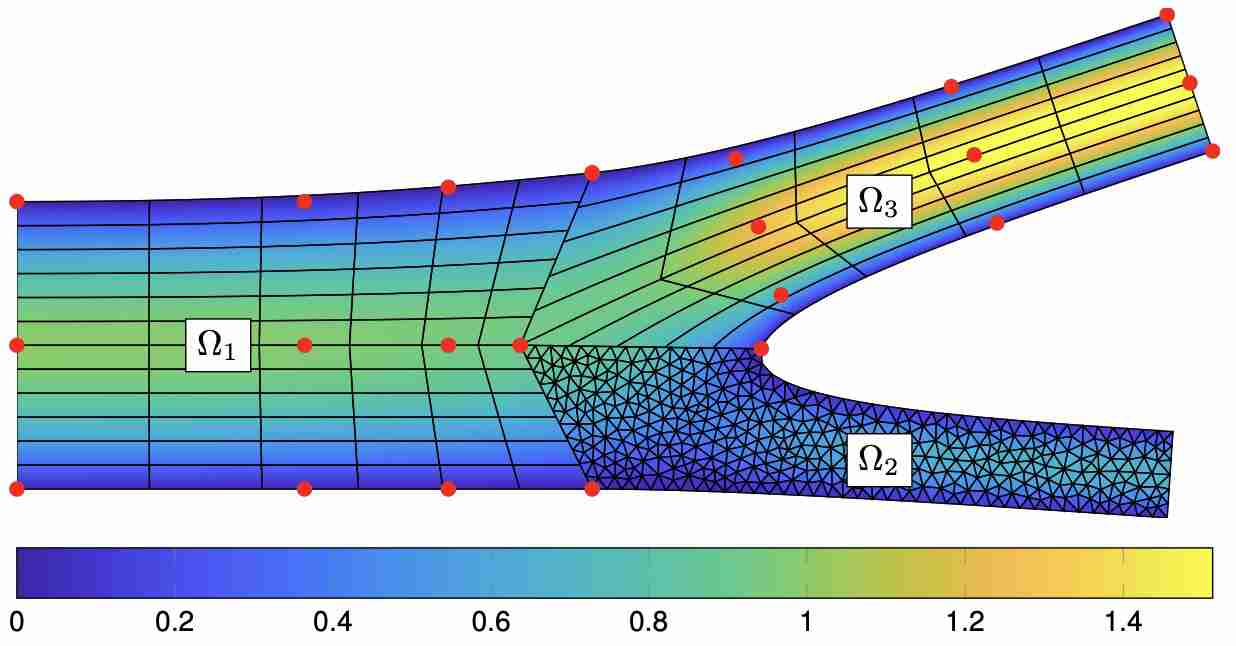
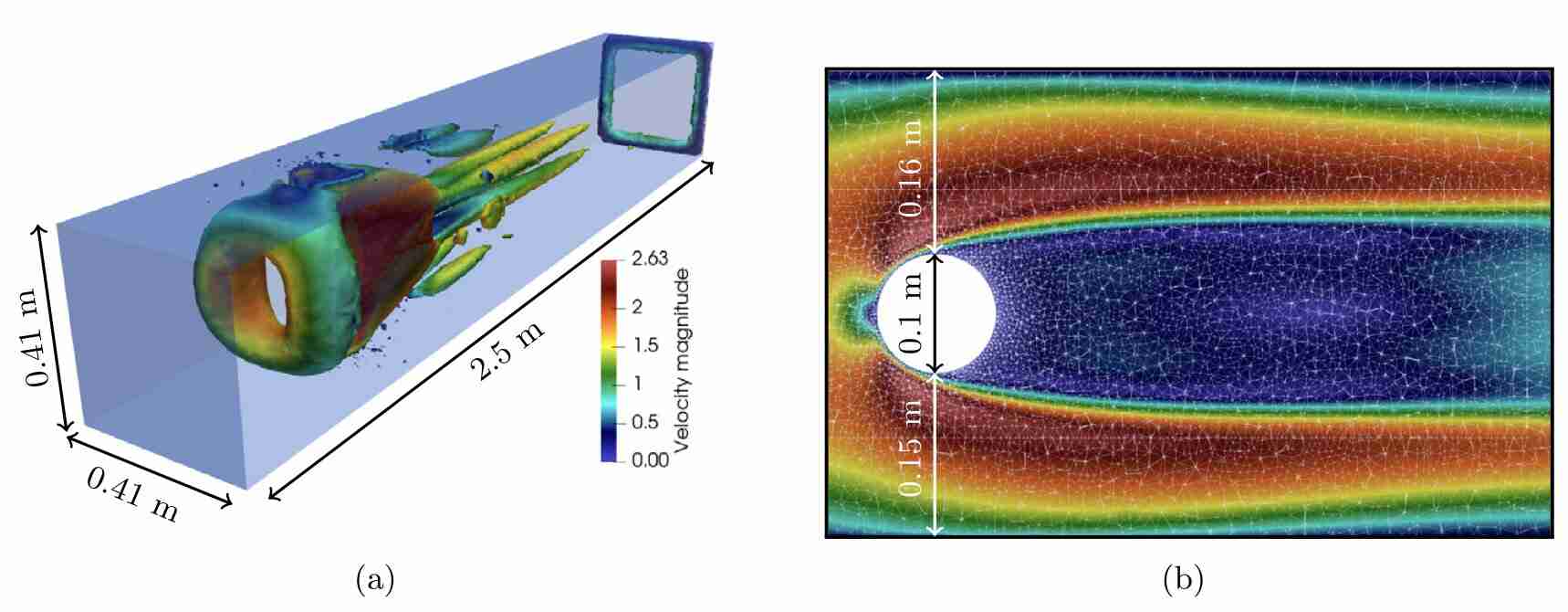
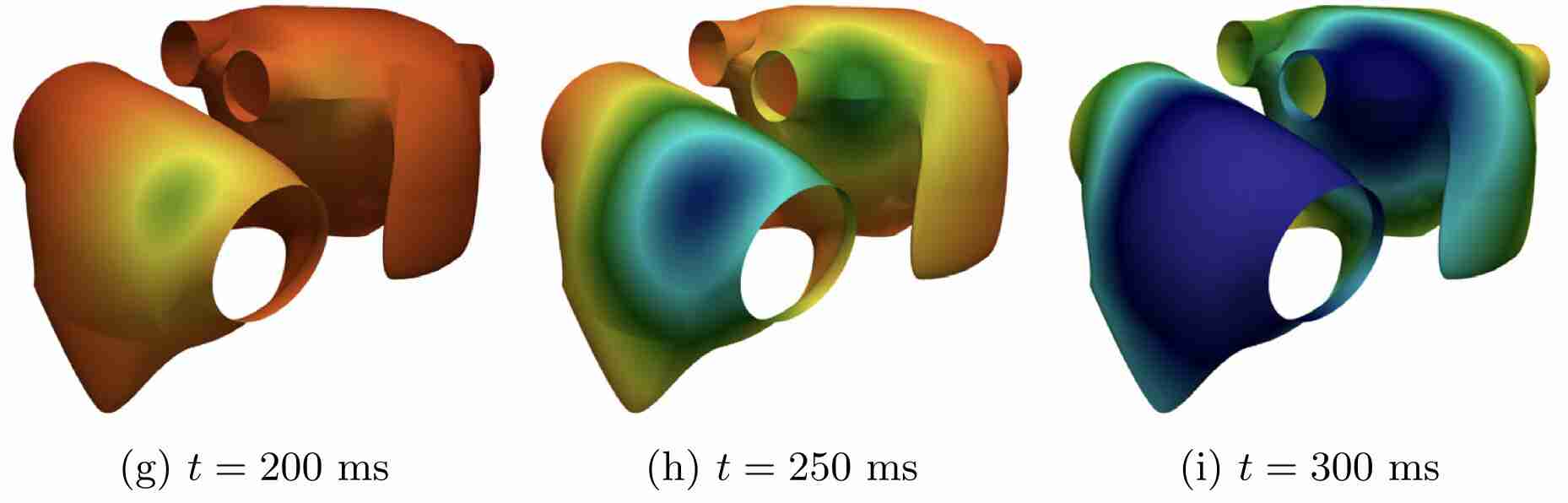
Schwarz, E. L., Pegolotti, L., Pfaller, M. R., & Marsden, A. L. (2023). Beyond CFD: Emerging methodologies for predictive simulation in cardiovascular health and disease. Biophysics Reviews, 4(1).
[
Paper
]
[
Abstract
]
Physics-based computational models of the cardiovascular system are increasingly used to simulate hemodynamics, tissue mechanics, and physiology in evolving healthy and diseased states. While predictive models using computational fluid dynamics (CFD) originated primarily for use in surgical planning, their application now extends well beyond this purpose. In this review, we describe an increasingly wide range of modeling applications aimed at uncovering fundamental mechanisms of disease progression and development, performing model-guided design, and generating testable hypotheses to drive targeted experiments. Increasingly, models are incorporating multiple physical processes spanning a wide range of time and length scales in the heart and vasculature. With these expanded capabilities, clinical adoption of patient-specific modeling in congenital and acquired cardiovascular disease is also increasing, impacting clinical care and treatment decisions in complex congenital heart disease, coronary artery disease, vascular surgery, pulmonary artery disease, and medical device design. In support of these efforts, we discuss recent advances in modeling methodology, which are most impactful when driven by clinical needs. We describe pivotal recent developments in image processing, fluid–structure interaction, modeling under uncertainty, and reduced order modeling to enable simulations in clinically relevant timeframes. In all these areas, we argue that traditional CFD alone is insufficient to tackle increasingly complex clinical and biological problems across scales and systems. Rather, CFD should be coupled with appropriate multiscale biological, physical, and physiological models needed to produce comprehensive, impactful models of mechanobiological systems and complex clinical scenarios. With this perspective, we finally outline open problems and future challenges in the field.